This calculator uses Cochran’s formula to calculate the minimum sample size for a study. It works for both infinite and finite populations by using the confidence level, margin of error, and population proportion. When a population size is provided, the calculator applies the finite population correction (FPC). In addition to the final result, it shows clear step-by-step calculations. This helps you to learn how to apply Cochran’s formula manually.
What is Cochran’s Formula?
Cochran’s formula is a statistical formula used to estimate the minimum sample size needed for a survey or research study. It is especially useful when you want to estimate a population proportion, and the population is large or unknown.
For an infinite population, Cochran’s formula is:
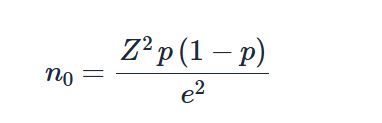
Where:
- n0 is the minimum sample size
- Z is the standard normal value corresponding to the chosen confidence interval. For instance, if you want to be 95% confident, the corresponding z value from the standard normal table is 1.96.
- p is an estimate of the population proportion
- e is the margin of error.
However, when the population size is known and relatively small (finite), we need to adjust the Cochran’s formula using the Finite Population Correction (FPC). This correction helps ensure that the sample size is not larger than necessary.
Therefore, for a finite population, the sample size formula using the Cochran’s method becomes:
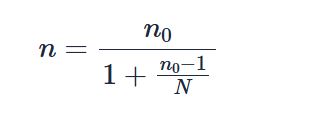
Where:
- n is the final sample size for a finite population
- n0 is the sample size obtained after applying Cochran’s formula for an infinite population.
- N is the total population size
Note. You should use the finite population correction only when the sample makes up a noticeable portion of the population (commonly when the sample exceeds about 5% of the population). In this case, the correction leads to a more accurate and realistic sample size.
When Should You Use Cochran’s Formula?
Not every study needs a complex sample size method. Cochran’s formula is a solid choice when your goal is simple: estimate a population proportion with a known level of accuracy.
You should use Cochran’s formula when:
- You want to estimate a population proportion (for example, the percentage of people who prefer a product or support an opinion).
- You are working with a large or unknown population and need an initial sample size estimate.
- You know your desired confidence level and margin of error.
- You have an estimated population proportion (p) or want to use 0.5 for a conservative estimate.
- You know the population size and want to apply the finite population correction (FPC) for more accurate results.
How to Compute Sample Size Using Cochran’s Formula: Example
Want to learn how to compute the sample size using Cochran’s Formula by hand? Let’s walk through an example.
Suppose a researcher wants to survey the proportion of people in a city who prefer electric cars. They want to be 95% confident with a 5% margin of error. Assuming that 50% of the people prefer electric cars and the total population size is unknown, we can compute the sample size as follows:
- Step 1: Identify the values
From the scenario, we know that:
- Confidence level = 95%. The corresponding z value is 1.96
- Margin of error = 0.05
- Estimated population proportion = 0.5
- Step 2: Apply Cochran’s formula for an infinite population
For an infinite population, the Cochran’s formula is:
Substituting the values in the formula, we have:
$$n_0 = \frac{1.96^2 \times 0.5 \times (1 – 0.5)}{0.05^2} $$
$$= \frac{3.8416 \times 0.25}{0.0025} $$
$$= \frac{0.9604}{0.0025} $$
= 384.16
Rounding up the answer to the nearest whole number, the minimum sample size becomes 385 participants.
Next, suppose that the city is known to have a population of 10,000 people. In this case, you should adjust the sample size using the finite population correction.
By definition, the Cochran’s finite population correction is:
But n0 = 384.16, N = 10,000.
Substituting the values in the formula and solving, we have:
Solving the equation and rounding up to the nearest whole number gives n = 370. This means that the researcher would need a sample of 370 people to achieve the same confidence and precision for a finite population.
Frequently Asked Questions (FAQs)
Cochran’s formula is a statistical formula used to calculate the minimum sample size required to estimate a population proportion with a given confidence level and margin of error.
For an infinite population, the formula is n₀ = Z²·p(1–p)/e². However, if the population is finite and known, the formula becomes n = n₀ / [1 + (n₀–1)/N].
You should use Cochran’s formula when you want to determine the minimum sample size for surveys or cross-sectional studies, especially when the population is large or unknown. For smaller, known populations, you should adjust the formula using the finite population correction to ensure an accurate sample size.
If the true population proportion is unknown, you should use p=0.5 because it produces a conservative (larger) sample size. However, if you know the population proportion for the study under investigation, make sure to use that.
Higher confidence levels require more precision, which increases the Z-value. This consequently leads to a larger sample size.
You should use the infinite population version when the population size is very large or unknown, and the sample makes up a small fraction of the total population.
Cochran’s formula is best used for studies that estimate proportions. It is not designed for estimating means or for complex sampling methods without modification.
